Dynamic salary
- Martin Schmalzried
- Mar 12, 2022
- 3 min read

Much ink has been spilled over the concept of “fair salary” or how to ensure that workers are fairly compensated for their job. In an ideal labour market, with a perfect balance of power between employers and job seekers, a fair salary should take the form of a “win-win” situation where the willingness of employers to pay for a job should meet the willingness of job seekers to take up a job. Unfortunately, in our current system, salaries are distorted by many mechanisms including:
Favouring capital over labour (dividends and investors over salaries and workers);
Employment blackmail (putting people in life threatening situations where they can barely meet their most basic needs, which makes them desperate for finding any source of income);
Sexism and discrimination (via non-transparent salary practices, employers can get away with paying women, migrants, minorities, less than other job seekers with a similar profile/expertise/qualification).
A transparent and dynamic salary offer could provide a solution to these problems and ensure that both employers and job seekers enter into a win-win agreement.
The proposed solution would function as follows:
An employer would set a minimum and maximum salary for a job or a task, as well as a deadline at which time the job offer would expire.
The employer would also set a maximum number of candidatures for a job. Once that number is filled, the job offer automatically expires.
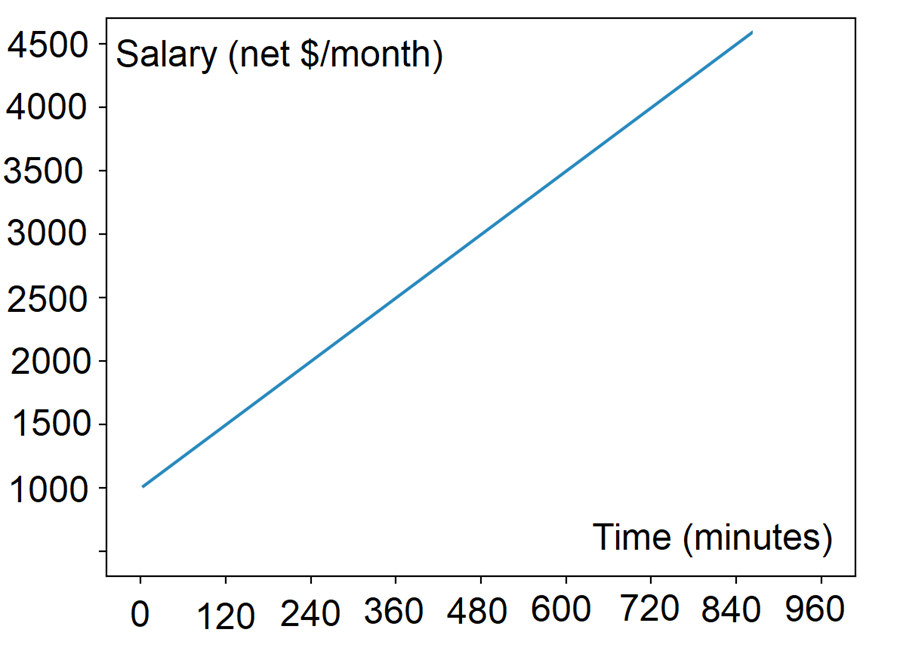
Upon publishing the job offer, the salary is adjusted dynamically by increasing the salary from the set minimum every minute until the deadline, where the salary reaches the maximum set by the employer.
Job seekers can submit their candidature at any time until the maximum number of candidatures are filled.
Formula:
Salary = minimum salary + ((Maximum salary — minimum salary) . elapsed time / Total time)
Salary = the dynamic change in salary proposal.
Minimum salary (m) = the base salary you are willing to propose.
Maximum salary (M) = the maximum salary you are willing to pay.
Elapsed time (t) = the time elapsed between the current time and the time you posted the job.
Total time = the total time between the initial posting of the job and the expiration of the job offer.
S = m + ((M-m). t/T)
The algorithm can be tweaked in various ways such as making it exponential rather than linear.
Example :
Salary = 1000€ + ((5000–1000€) . 250 minutes/6000 minutes) = 1166€
The salary for a job went from 1000€ to 1166€ after 250 minutes of being initially published. After the total time has elapsed (6000 minutes), the salary will be at 5000€.
Advantages:
Such a system has several advantages:
It allows job seekers to wait until the salary has reached a value which is subjectively perceived as fair, given their personal assessment of their merit, their qualifications/experience/expertise.
It creates a better allocation of labour based on willingness to engage in a specific task, ensuring that employers receive applications from motivated job seekers rather than desperate job seekers, which will in turn increase productivity, and overall well-being of workers.
It is transparent and open.
It provides key information about the state of the labour market balance and equilibrium. If job offers receive too many bids in the lower salary spectrum, it might indicate a surplus of workers and a shortage of jobs. If the job offers receive too little bids and only in the higher salary spectrum, it might indicate a shortage of workers and too many jobs being offered. Such data could be used to rebalance the labour market via various levers (training, seeking labour from outside the community, encouraging the publication of more job offers etc.)
It allows employers to make informed choices about picking candidates, matching their budgetary constraints with their need for a qualified and competent work force.




Comments